Table of contents
Hey folks, as said in the introductory blog I will start a series on the mathematics involved in computer science, here is the first blog of the series on Time Complexity which many of you have heard or read about and some of you might be thinking that there's a lot of content out there, so why here's another adding to the bulk. So the reason is that the purpose of the series is not to teach things but to make things beginner-friendly, fun, and interesting so that real-world applications can be easily seen or explored.
So let's dive into the topic and make it easy for everyone.
Q. What is Time Complexity?
Time complexity is not equal to the time taken by any machine to run an algorithm or produce an output.
But it is actually -"The function that gives the relationship between time and size of input for an algorithm i.e. about how the time will grow as the size of the input grows."
The definition doesn't explain much about it, there's still a lot of fog that has to be cleared. So to clear the fog let's first look at some things that need a bit of attention, in this blog we mostly are considering the examples and comparisons of Linear Search and Binary Search as most beginners are familiar with them.
Best Case Analysis- This can be defined as the cases in which, for some inputs, any algorithm performs its task perfectly and very efficiently and for these cases, the computation time of an algorithm is calculated.
For Ex: If you try to search for an element in an array using linear search which starts searching from the beginning and goes till the end, if the element is found at the very first index (i.e. 0th position); isn't it the best case for linear search? The same goes for binary search that the target we're trying to search is in the middle of the array and getting encountered at the beginning of the search. So these kinds of inputs contribute to the best case analysis.
Average Case Analysis- For this, we take all the possible cases, calculate the computation time, sum them up and divide them by the no. of cases. For this, we need to see the distribution of each input contributing to the analysis, which is a kind of a mess.
Worst Case Analysis- To consider the worst cases for an algorithm, we try to find the edge cases (these are the cases for which the algorithm might not work correctly, or give wrong output or anything) associated with it or the cases for which the algorithm takes the maximum time to give the output.
For Ex: If we try to search for an element in an array using linear search, the pointer goes to the end of the array to find the element but the element doesn't exist in the array. Similarly, in binary search, to find the target, the array got divided into half repeatedly, and at the end, only one element was left which wasn't equal to the target element. So these cases contribute to the worst case analysis.
Now let's look at one last thing and we'll be ready to get into that time complexity thing.
The Big-Oh Notation: This notation gives the upper bound of an algorithm or describes the complexity of an algorithm in an algebraic expression. It is represented by - O(algebraic expression).
Upper-bound of an algorithm is the maximum limit that can't be exceeded for any input which is the Time Complexity of an algorithm. For example, consider an array of 6 elements - [1, 5, 2, 7, 11, 6], we have to search for the key which is 12. So linear search makes 6 comparisons to search for 12 in the array but the element is not found because it doesn't exist in the array, so the upper bound here is 6 comparisons. Similarly for an array of N elements, the upper bound would be O(N) and so is the Time Complexity.
Note: Time Complexity for binary search is O(logN).
Constant Time Complexity: If an algorithm's time complexity is constant, it doesn't matter what the input size is, the algorithm will run in the same amount of time for some inputs. For example, if you want to get the first element of an array, the size of the array will not matter in this case. It is represented by O(1).
So, these were some topics you needed to know to have a better understanding of Time Complexity.
Significance of Time Complexity :
Let's compare the Time Complexity of Linear Search and Binary Search:
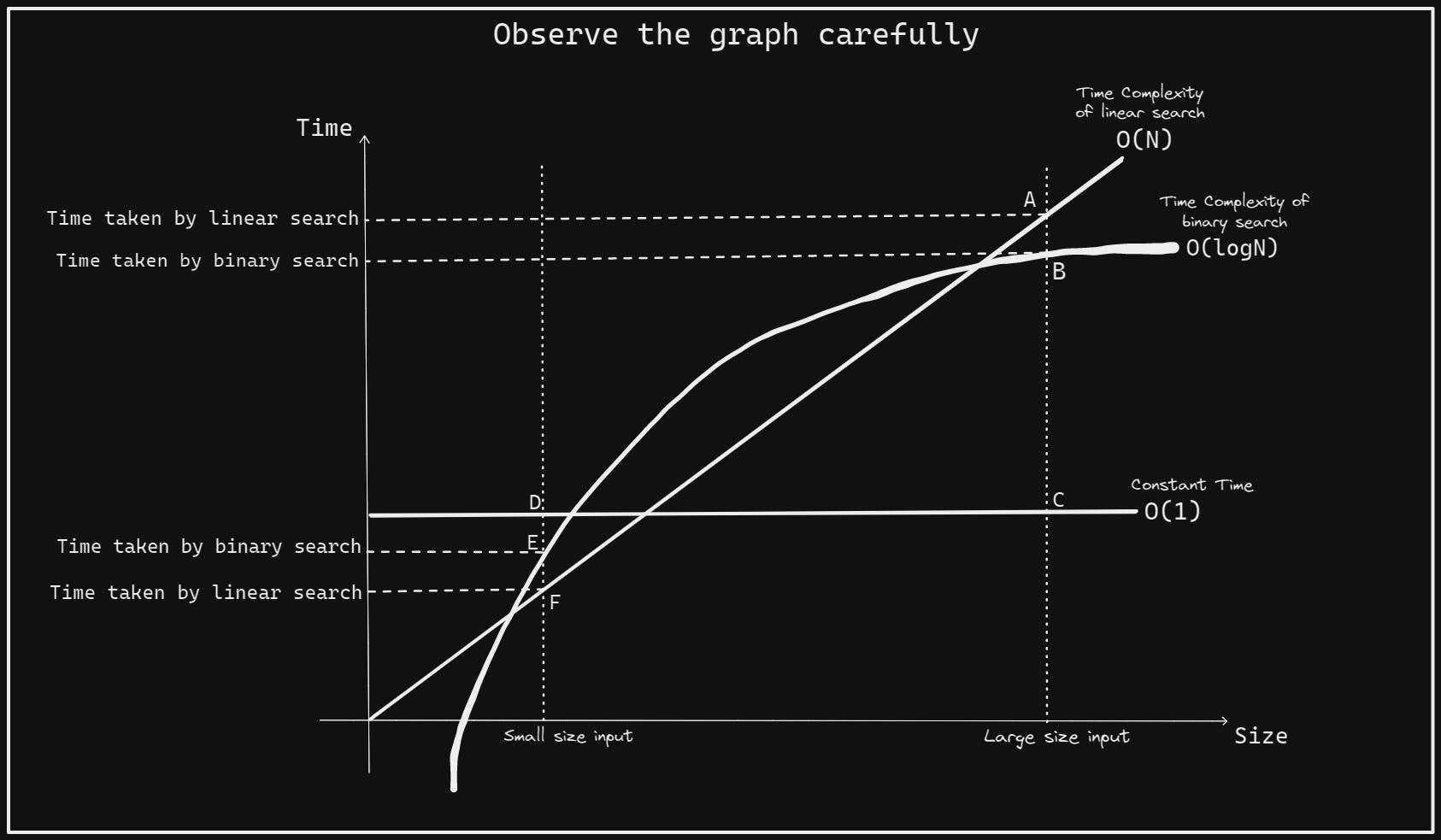
On observing the graph we can have an abstract idea about these complexities; it can be seen that for small-sized input, point E is at a higher position than point F which means the time taken by binary search to process small-sized input might be more than linear search for some cases but point D is even higher which means that the constant time taken to process some inputs might be more than the time taken by both these algorithms.
But we must understand that we don't have to worry about small-sized inputs or how much time the algorithm is taking. The real problems to be taken into consideration are large-sized inputs because in the real world we try to consider what's the worst thing that could happen with the algorithm. So we focus on the worst-case complexities.
Let's look at the graph again for large-sized inputs, it can be inferred that the constant time will always be less; due to the logarithmic time complexity, binary search will take much lesser time than linear search to search for an element in an array.
Therefore, Time Complexity : O(1) < O(logN) < O(N).
Hence, we can analyze the efficiency of an algorithm by looking at its time complexity.
Now the question comes is that,
What all things should we consider while thinking about the time complexity for an algorithm?
- Always look for the worst-case complexity.
- Always look at complexity for large or infinite data (points 1 & 2 are interrelated).
- To understand the relationship:
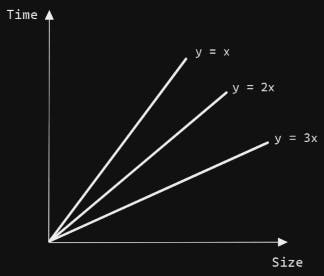
a. Even though the value of actual time is different (according to the graph) but they are all growing linearly i.e. the relationship is linear.
b. But we don't care about the actual time taken by the algorithm, we care only about the relationship.
c. So we ignore all the constants and less dominating terms to obtain the time complexity. Now, the question comes, why is it necessary less dominating terms?
This can be proved via an example:
Consider the time complexity : O(N³ + logN)
Taking large data according to point (2) mentioned above i.e. N = 1million = 10⁶
=> O( (10⁶)³ + log(10⁶) ) = O( (10⁶)³ + 6 (log10) ) = (10⁶)³ sec.+ 6 sec.
but, (10⁶)³ >>> 6.
Hence less dominating terms can be ignored and O(N³ + logN) = O(N³).
As the module suggests transparently that mathematics is an integral part of the fundamentals of computer science. Time Complexity involves the basic concepts of functions like polynomial, logarithmic functions, exponential functions, etc.; or the intuition of pattern recognition using graphs and other mathematical calculations.
So, folks, this was all about Time Complexity that y'all needed to know. The upcoming topics will be interrelated, so if you have any queries or doubts about this one please let me know on my social handles so that you can enjoy the upcoming one.
Twitter : Shashwat_g27 | Instagram : shashwat_g27 | LinkedIn : shashwat
Thank you for reading and stay tuned ❤️.
